【DFS式的枚举】看了大佬的题解，一步步优化了自己的算法

题目描述

思路

像这种求一个个具体方案的题，大概率都是用递归+其他算法去求的。这道题也没什么例外，要看一个数x能不能找到另外几个数，加和成为target，就要看接下来的数能不能凑成target-x。一直向下递归，直到某一层target==0，此时的方案就是可行的。

这种DFS式的搜索相当像一棵树，对于我们而言，只有target==0的叶节点到根节点的路径是正确的方案之一。

解题方法

根据以上的思路，我们就能写出一般的DFS枚举搜索。很幸运的是，这题不加剪枝的暴搜是可以过的。

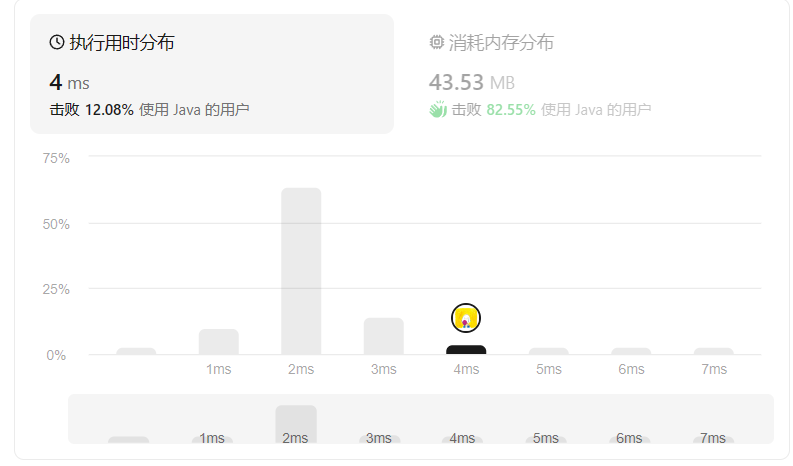
而对于不限定数组内元素顺序的题目，我们可以排个序，在接下来的DFS中，如果当前的数candidates[i]已经使得target-candidates[i]<0了，后面的所有数也不需要考虑了，差值一定都小于0，都是非法的。

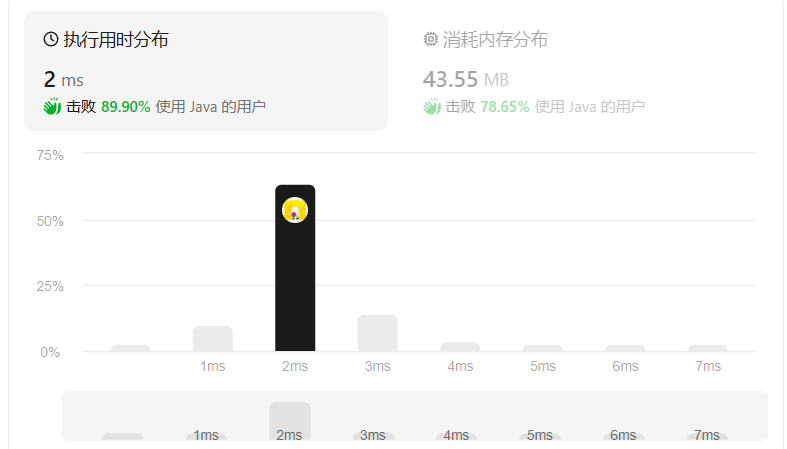
今天才知道，Java当中也有双端队列Deque，这同样可以优化时间复杂度，但对于一个已经排好序的数组来说，效果不是很明显。

复杂度

时间复杂度:自己粗略算了一下 ，应该是O(n+n/2+n/3+……+1)=O(n)

空间复杂度:就是递归最大深度，O(n)

Code

class Solution {
    private Deque<Integer> list=new ArrayDeque<>();    
    private List<List<Integer>> ansList=new ArrayList<>();

    public void DFS(int nx,int[] candidates,int target){
        if(target==0){
            ansList.add(new ArrayList<>(list));
            return ;
        }
        for(int i=nx;i<candidates.length;i++){
            if(target-candidates[i]<0)break;
            list.add(candidates[i]);
            DFS(i,candidates,target-candidates[i]);
            list.removeLast();
        }
    }

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        Arrays.sort(candidates);
        DFS(0,candidates, target);
        return ansList;
    }
}