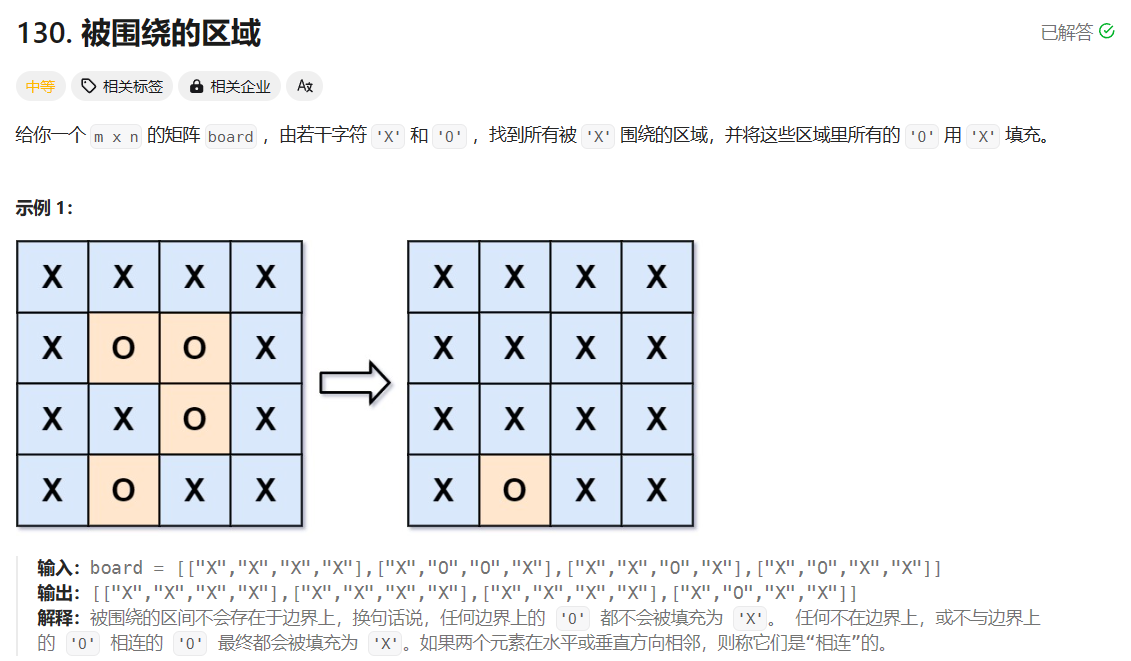
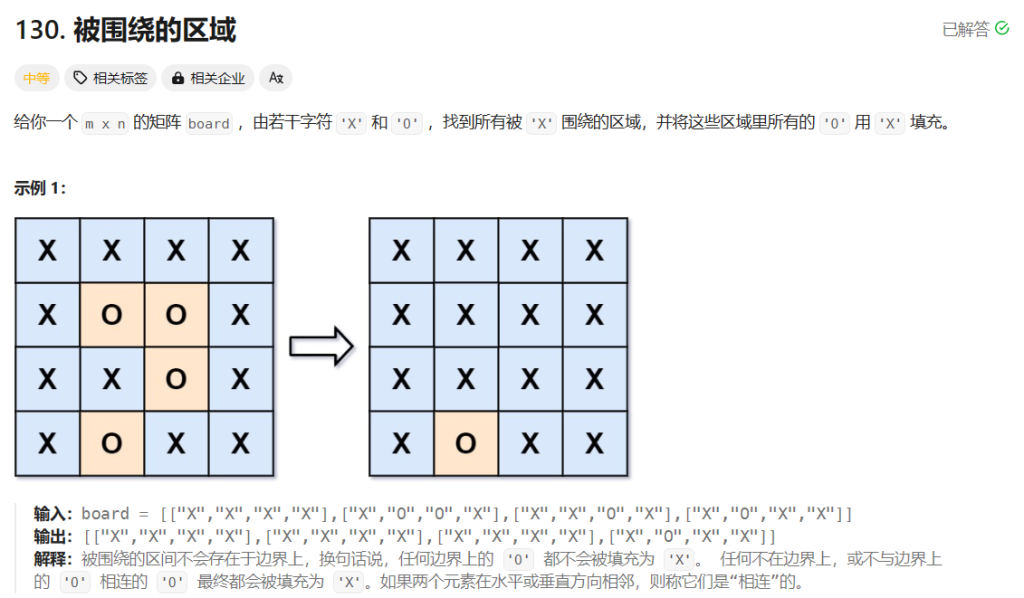
题目描述

思路

就如标题所言，不在边界的、或者不跟边界连通的O区域肯定会被围绕，那么我们只需要先遍历所有边界O区域（处在边界，或者跟边界能够通过O来连通的、只由O组成区域），并将其标记。之后我们对每一个O都检查一遍，没有被标记的就一定会被围绕，涂成X.

解题方法

思路很简单，代码也很好写。如何遍历所有边界O区域,我们写这样四个循环就可以了。这里的标记，可以等效于访问标记vis。

//首行
for(int j=0;j<n;j++)if(board[0][j]=='O'&&vis[0][j]==false)DFS(0,j,board);
//尾行
for(int j=0;j<n;j++)if(board[m-1][j]=='O'&&vis[m-1][j]==false)DFS(m-1,j,board);
//首列
for(int i=0;i<m;i++)if(board[i][0]=='O'&&vis[i][0]==false)DFS(i,0,board);
//尾列
for(int i=0;i<m;i++)if(board[i][n-1]=='O'&&vis[i][n-1]==false)DFS(i,n-1,board);

只要没有被标记的，就一定不是边界O区域，那就一定会被X围绕。

for(int i=0;i<m;i++){
    for(int j=0;j<n;j++){
        if(board[i][j]=='O' && vis[i][j]==false)board[i][j]='X';
    }
}

复杂度

时间复杂度: 因为只是两遍图的遍历，所以O(mn+mn)O(mn+mn)O(mn+mn)=O(mn)O(mn)O(mn)

空间复杂度: 需要有有一个标记数组vis，所以O(mn)O(mn)O(mn)

完整代码

class Solution {
    private int[] dy={1,-1,0,0};
    private int[] dx={0,0,1,-1};
    private boolean[][] vis=new boolean[205][205];
    private int m,n;
    public void DFS(int x,int y,char[][] board){
        vis[x][y]=true;
        for(int k=0;k<4;k++){
            int nx=x+dx[k],ny=y+dy[k];
            if(nx<0 || nx>=m || ny<0 || ny>=n || vis[nx][ny]==true || board[nx][ny]=='X')continue;
            vis[nx][ny]=true;
            DFS(nx,ny,board);
        }
    }
    public void solve(char[][] board){
        m=board.length;
        n=board[0].length;
        //从边界区块开始DFS
        //首行
        for(int j=0;j<n;j++)if(board[0][j]=='O'&&vis[0][j]==false)DFS(0,j,board);
        //尾行
        for(int j=0;j<n;j++)if(board[m-1][j]=='O'&&vis[m-1][j]==false)DFS(m-1,j,board);
        //首列
        for(int i=0;i<m;i++)if(board[i][0]=='O'&&vis[i][0]==false)DFS(i,0,board);
        //尾列
        for(int i=0;i<m;i++)if(board[i][n-1]=='O'&&vis[i][n-1]==false)DFS(i,n-1,board);

        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(board[i][j]=='O' && vis[i][j]==false)board[i][j]='X';
            }
        }
    }
}