1. 函数签名与参数
pub fn rms_norm(y: &mut Tensor<f32>, x: &Tensor<f32>, w: &Tensor<f32>, epsilon: f32) {
...
}y: 输出张量(可变),用于存储归一化后的结果。x: 输入张量,待处理的数据。w: 权重张量,应用于每个元素的缩放。epsilon: 小的正数,用于防止 RMS 值为零时的数值不稳定问题。
2. 参数校验
assert_eq!(x.shape(), y.shape(), "Input and output tensors must have the same shape.");
assert_eq!(x.shape().last(), w.shape().last(), "Weight tensor must have the same size as the last dimension of input tensor.");- 相同形状校验:确保输入和输出张量
x和y的形状相同,确保每个输入元素有对应的输出位置。 - 权重校验:确保权重张量
w的大小与输入张量x的最后一个维度的大小相同。这是因为 RMS Normalization 是在最后一个维度上进行的,而权重应用于每个元素。
3. 准备批次处理
let num_elements = x.length();
let last_dim_size = *x.shape().last().clone().unwrap(); // 得到最后一个维度的大小,即长度 n
let num_batch = num_elements / last_dim_size; // 计算批次数量- 元素数量:
num_elements表示张量x中的总元素数量。 - 最后维度大小:
last_dim_size为n,表示最后一个维度的大小,即每个子向量的长度。 - 批次数量:
num_batch计算出一共有多少个批次,每个批次为一个长度为n的向量。
4. 遍历批次进行计算
for batch_idx in 0..num_batch {
let start_idx = batch_idx * last_dim_size;
let end_idx = start_idx + last_dim_size;
// 提取当前批次的数据并计算平方和
let batch_data = &x.data()[start_idx..end_idx];
let sum_of_sequence: f32 = batch_data.iter().map(|&value| value * value).sum();- 批次索引:通过
batch_idx遍历每一个批次。 - 批次边界:
start_idx和end_idx确定了当前批次在数据中的起始和结束索引。 - 提取批次数据:
batch_data是当前批次的数据切片。 - 平方和计算:
sum_of_sequence计算当前批次的所有元素的平方和。
5. 计算 RMS 值
let rms = (sum_of_sequence / last_dim_size as f32 + epsilon).sqrt();RMS 计算:RMS 值通过计算平方和的平均值,然后取平方根,再加上一个小的正数 epsilon 来稳定计算。
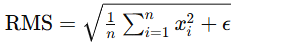
6. 执行归一化并应用权重
for i in 0..last_dim_size {
let weight = &w.data()[i]; // 权重应用于每个元素
unsafe { y.data_mut()[start_idx + i] = batch_data[i] * weight / rms; }
}
}- 遍历批次元素:在当前批次内,遍历每个元素进行归一化。
- 权重应用:
weight作为缩放因子应用于每个元素。 - 归一化计算:更新输出张量
y中每个元素为:
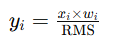
- 使用
unsafe:直接访问和修改输出张量的内部数据。这种操作要求开发者保证访问的安全性。
7. 函数调用示例
下面是如何使用 rms_norm 函数的一个简单示例:
fn main() {
// 初始化示例张量
let input_data = vec![0.5, 0.6, 0.7, 0.8, 0.9, 1.0];
let weight_data = vec![1.0, 1.0, 1.0];
let shape = vec![2, 3]; // 示例张量形状为 2x3
let x = Tensor::new(input_data.clone(), shape.clone());
let w = Tensor::new(weight_data, vec![3]);
let mut y = Tensor::new(vec![0.0; input_data.len()], shape);
// 调用 rms_norm 函数
rms_norm(&mut y, &x, &w, 1e-8);
// 输出归一化结果
println!("Normalized Tensor: {:?}", y.data());
}解释总结
- 输入与输出准备:确保输入、输出和权重张量的形状匹配。
- 批次计算:针对张量的最后一维度,每个子向量作为一个批次进行处理。
- RMS 计算:使用均方根公式计算每个批次的 RMS 值。
- 归一化与权重应用:调整每个元素的值以实现归一化,并应用给定的权重。
- 结果存储:将计算结果存储在输出张量中。
完整代码
pub fn rms_norm(y: &mut Tensor<f32>, x: &Tensor<f32>, w: &Tensor<f32>, epsilon: f32) {
assert_eq!(x.shape(), y.shape(), "Input and output tensors must have the same shape.");
assert_eq!(x.shape().last(), w.shape().last(), "Weight tensor must have the same size as the last dimension of input tensor.");
let num_elements = x.length();
let last_dim_size = *x.shape().last().clone().unwrap();//也就是提示当中提到的n
let num_batch = num_elements/last_dim_size;//得到究竟有多少批次
//“即张量 X(...,n)和 Y(...,n)都是由若干个长度为n的向量xi,yi组成的”
for batch_idx in 0..num_batch{
let start_idx = batch_idx*last_dim_size;
let end_idx = start_idx+last_dim_size;
//提前当前批次的所有数据,并计算出平方和
let batch_data = &x.data()[start_idx..end_idx];
let sum_of_sequence:f32 = batch_data.iter().map(|&value| value*value).sum();
//计算本批次的RMS
let rms = (sum_of_sequence/ last_dim_size as f32+epsilon).sqrt();
//得出本批次的RMS Normalization
for i in 0..last_dim_size{
let weight =&w.data()[i];//说明了w就是一个一维向量
unsafe { y.data_mut()[start_idx + i] = batch_data[i] * weight / rms; }
}
}
}这种实现方式在处理大规模数据时特别有效,因为它能够利用批处理模式优化计算效率,并支持复杂张量的多维度操作。Rust 的类型系统和内存安全特性提供了安全而高效的数值计算能力。