在以往的练习当中,贪心更多是一种思想,且常常在求解最优解的时候会自然而然地想到——然而,尽管贪心这种“显然易见”的特性能够在一些场合中推出全局最优解,但最好还是要经过一番论证(常见的证伪方式是举反例来说明贪心并不能得出最优解)。
而双指针,更多作为一种工具,多用在中低难度的题目当中。双指针主要有两种形式,一种是同侧,一种是异侧(两个边界端点)。
这里选出几道cf上比较好的题目,剖析出其中比较重要的知识点。
Beta Round #6 – Task Analysis—C. Alice, Bob and Chocolate
就是两个人从两侧吃巧克力棒的问题,很明显就是让你去用双指针了,但是需要额外特别在意两指针的边界问题。从题目所给信息来看,我们就有两条约束原则:
- 倘若Alice和Bob都将同时拿到巧克力棒
i,这根巧克力棒i将属于Alice - 正在被另一个人吃的巧克力棒,下一时刻就不能再被另一个人吃了,即先来先得。
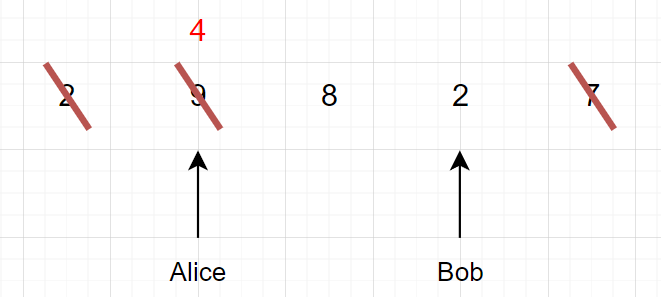
因此我们的循环条件应该这样写:
if(left==right)Alice=1,Bob=0;
else{
while(left+1<right)
{
if(a[left]<a[right]){
a[right]-=a[left];left++;
}else if(a[left]>a[right]){
a[left]-=a[right];right--;
}else{
if(right!=left+2)left++,right--;
else left++;
}
}
Alice=left,Bob=n-right+1;
}CodeTON Round 7 (Div. 1 + Div. 2, Rated, Prizes!) Editorial—1896B – AB Flipping
这道题简单,但很有意思。根据题意,我们分析进行一次操作的条件,不难推理出所有在B前面的A最后都将被移到B后面去,并且,一旦交换操作发生(从前往后一直接龙),一直到再遇到A为止,这个过程中经过的位置都不能再被使用(因为题目说了下标只让用一次)。
这里其实就不知不觉地使用了贪心,因为我们已经分析出了交换操作的必要条件——即运用最少操作就可以让A全都移到B的后面。
int tail=0,sum=0;
for(int i=1;i<=n;i++){
if(s[i]=='B'){
sum+=tail;
tail=min(tail,1);
}else tail++;
}只关乎开始与结束两状态的抽象思维
我把这一类的抽象简称为一层抽象
在练习贪心和双指针的题目的时候,刷到几道使用一层抽象要更容易解决的题目,这里简单列出思路。
Educational Codeforces Round 148 Editorial—B. Maximum Sum
两个关键点:
- 我们根本不需要知道过程发生了什么。经过排序,删除最小数一定发生在队首,删除最大数一定发生在队尾,因此次数就决定了过程是什么样的。
- 删除两个最小数和删除一个最大数的次数总和为k,那么知道了删除其中一者的次数,就一定能知道另一者的次数。二维化一维,直接枚举就是。
sort(a+1,a+1+n);
for(int i=1;i<=n;i++)pre[i]=pre[i-1]+a[i];
ll ans=0;
for(int m=0;m<=k;m++){
ans=max(ans,pre[n-(k-m)]-pre[2*m]);
}Codeforces Round 955 (Div. 2, with prizes from NEAR!) Editorial—A. Soccer
我们只看开始与结束,假如A队一开始就处于领先状态,结束的时刻却不再处于领先状态,就足以说明过程中一定经历了平局(自己想一想是不是?),反之,A队开始和结束两个时刻都处于领先状态,当然就存在一直不平局的解(即可以不经历平局)。对于B队也是同样的道理。
if(sa>sb){
//如果A队一开始就处于领先状态
//结束的时候不再处于领先状态
//就必然要经历平局状态
if(ea<eb){
cout<<"NO"<<endl;
}else{
cout<<"YES"<<endl;
}
}//对于B队,也是同样的道理
else if(ea>eb){
cout<<"NO"<<endl;
}else cout<<"YES"<<endl;尾声
也不知道是不是基础算法的缘故,上面这几道题的最好的解法并不是使用贪心/双指针,而是推理/思维,这或许就是算法的玄学吧——固有的方法论并不可靠,具体的题目必须要经过具体的分析,抽象出一般规律,再加上一点思维的火花,才能得以解决。

