【蓝桥国赛】抓娃娃——逻辑索引映射+前缀和

原题信息

思路分析

我们的研究对象都是一条条线段，这个是相当不太好求的，因为要确定一条线段，就必须知道它的两个端点，相当于有两个变量l与r。那么我们能不能简化一点，减少变量呢？

其实是可以的！只要我们求出每条线段的中点，就可以代表这条线段，并且还是唯一的，还可以仅凭中点就立马判断出某个区间是否覆盖了这条线段的一半！那么这道题就顺利地转化为了求某个区间内的数量和，这不就是我们熟悉的前缀和问题吗？

但是，如果我们只是套用前缀和的模板写会出大问题，因为线段中点完全有可能是小数，而前缀和数组的索引都是整数，如果还是用prefix[R]-prefix[L-1]来求[L,R]区间包含的有效线段（即一半都在该区间的某条线段），就会出现下图说明的误差：

这里，我们定义prefix[i]为[1,i]区间内包含的有效线段数。

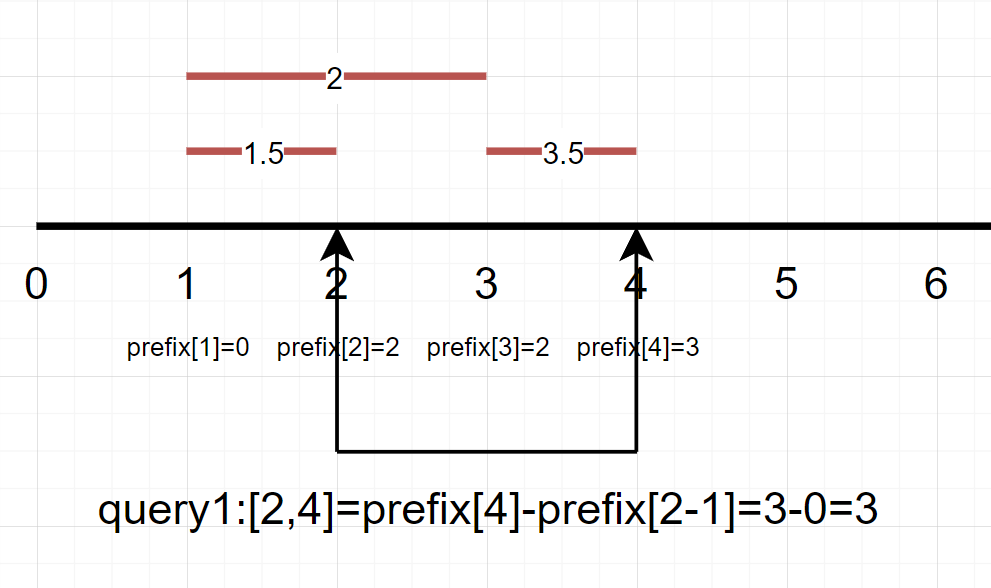
预期的答案应该是2呀！这样的求法，就把不属于区间[2,4]的、中点为1.5的线段[1,2]也纳入了进来，显然是不合理的。针对这个问题，方法其实是有很多的，这里我们采用最简单，也最好理解的方法，即将所有的实际索引*2，得到逻辑索引——这样就可以解决中点为小数的问题了。

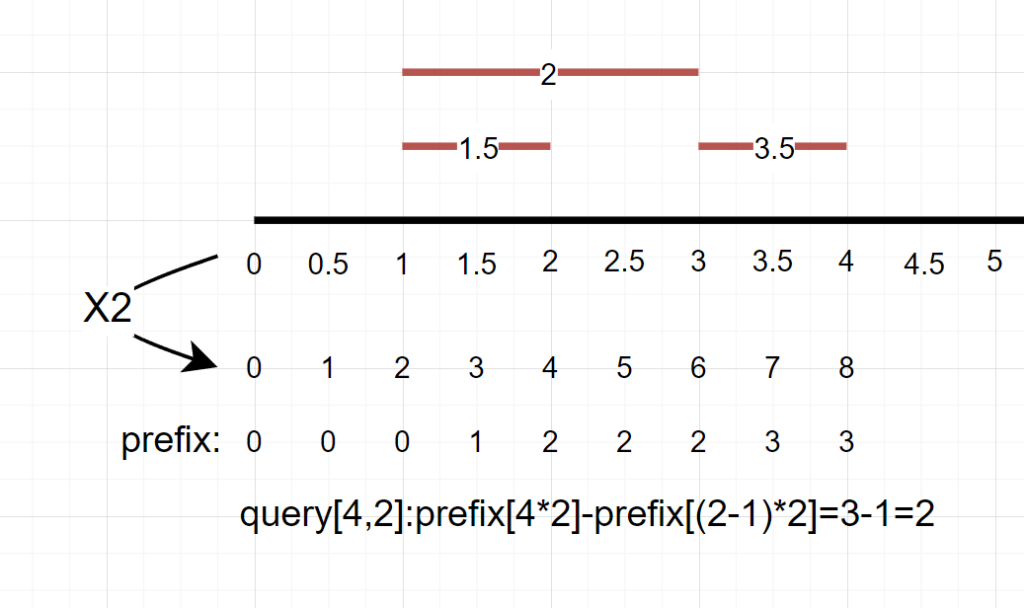
非常地nice，接下来就是完整代码实现，理解了将线段中点等价于线段和逻辑索引映射这两点后，代码就都好写了。

完整代码

#include<bits/stdc++.h>
using namespace std;
const int N=2e6+5;
int prefix[N];//[1,i]范围内涵盖的有效线段数
int n,m;
map<float,int> num_d;//记录各不同线段的个数(float) 
int main()
{
	cin>>n>>m;
	int l,r;
	for(int i=1;i<=n;i++){
		cin>>l>>r;
		float d=(l+r)/2.0;
		num_d[d]++;
	}
	
	prefix[1]=0;
	float i=1.5;
	for(;i<=N/2;i+=0.5){
		//逻辑索引映射
		int nowI=i*2,preI=(i-0.5)*2;
		prefix[nowI]=prefix[preI]+num_d[i];
	}
	int L,R;
	while(m--)
	{
		cin>>L>>R;
		//逻辑索引
		int logR=R*2,logL=(L-0.5)*2;
		cout<<prefix[logR]-prefix[logL]<<endl;
	}
 return 0;
}