【算法笔记】——树的直径问题，两种解法

写在前面

五一期间，参与CCPC校内选拔的热身赛的时候遇到了有关树的直径问题。掌握了如何解决树的直径问题，也就解决了如何在一个有向无环图中求得一条最长路径，而目前我所了解到的计算该问题的方法主要有两种，写篇文章记录之。

树的直径：一棵树/一张有向无环图中的最长路径

需要说明的是，本篇讨论的树（或者有向无环图）所说的路径长度指的都是权重和，如果不考虑权重和，其直径就更加好求，把每条边都赋予一个1的权重，就可以用一种方法统一处理。

树就是有向无环图，且用树来阐释会更方便，因此下文就主要用树作为主语，方法可以套用在任意一张有向无环图当中。

求法一：求每棵子树到底端的最长和次长路径

我们随便画一棵树，自己随意设定一条直径。在这里，我设下面这棵树的直径为GI，会发现无论选取那一条作为直径，它都必然附着于一棵子树上。

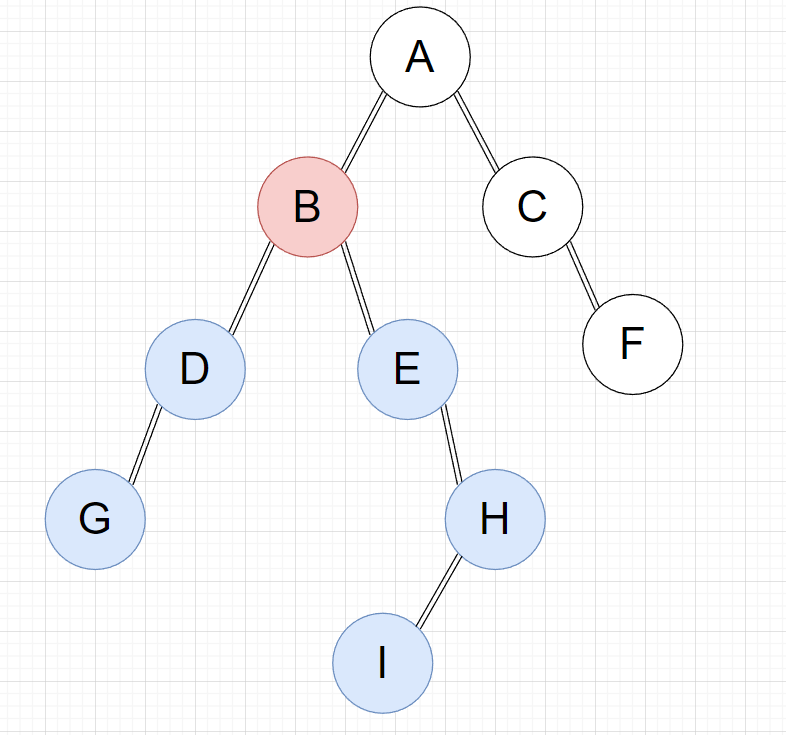
树的直径必然包含在某一棵子树的内，那该如何计算呢？其实就是该子树根节点到底端叶子节点的最长和次长路径之和。

因此我们只需要递归求解每棵子树到底端的最长和次长路径就可以了，代码如下：

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
typedef pair<int,int> PII;
typedef long long ll;

vector<PII> edge[N];
int dp[N];//dp[i]表示以i为根节点的子树到底端的最长和次长距离之和 
ll ans;
int DFS(int u,int fa){
	ll max1=0,max2=0;
	for(auto it:edge[u])
	{
		int v=it.first,w=it.second;
		if(v==fa)continue;
		dp[v]=DFS(v,u)+w;
		if(dp[v]>max1){
			max2=max1;
			max1=dp[v];
		}else if(dp[v]>max2){
			max2=dp[v];
		}
	}
	ans=max(ans,max1+max2);
	
	dp[u]=max1;
	return dp[u];
}

int main()
{
	int n;cin>>n;
	int u,v,w;
	for(int i=0;i<n-1;i++){
		cin>>u>>v>>w;
		edge[u].push_back({v,w});
		edge[v].push_back({u,w});
	}
	DFS(1,0);
	cout<<ans<<endl;
 return 0;
}

求法二：求出离根节点最远的结点node，再求离node最远的结点

这个方法是我知道的第一种方法，但是网上的论证不太充分，我并没有读懂，因此把它放在文章的后面，就当作一个小结论。

先求出距根节点最远的结点node1，再求出离node1最远的结点node2，node1与node2的路径就是树的直径，其长度也就是直径的大小。这其中有两次DFS，因此距离是需要计算两遍的

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+10;
ll dist[N];//dp[i]表示根节点到结点i的距离（权重和） 
vector<pair<int,int>> edge[N];
bool vis[N];
void DFS(int u,int fa){//fa是为了不走回头路 
	for(auto next:edge[u]){
		//next->pair<v,w>
		int v=next.first,w=next.second;
		if(v==fa)continue;
		dist[v]=dist[fa]+w;
		DFS(v,u);
	}
}

int main()
{
	int n;cin>>n;
	int p,q,d;
	for(int i=1;i<=n-1;i++){
		cin>>p>>q>>d;
		edge[p].push_back({q,d});
		edge[q].push_back({p,d});
	}
	DFS(1,0);
	//找到距离根节点最远的结点
	int node,len=0;
	for(int i=1;i<=n;i++){
		if(dist[i]>dist[node]){
			node=i;
		}
	}
	memset(vis,0,sizeof(vis));
	//以node为根节点，再DFS一遍，找到离node最远的结点
	dist[node]=0;
	DFS(node,0);
	for(int i=1;i<=n;i++){
		if(dist[i]>dist[node]){
			node=i;
		}
	}
	ll s=dist[node];
	ll cost=10*s+(1+s)*s/2;
	cout<<cost<<endl;
 return 0;
}